Mare lucru din matematica nu prea mai imi amintesc, desi a fost o vreme in care am mancat matematica pe paine. Olimpiade, Facultate de Matematica, chestii. Dar daca ma pui acum sa fac o integrala sau sa rezolv o problema de geometrie de a noua, ma fac de ras. Ar trebui sa o iau de la capat: sa-mi amintesc teoreme, sa rememorez formule.
Asta pentru faptul ca niciodata nu am stat bine cu memoria. Tin minte lucruri prin asocieri, de maniera vaga, fac legaturi uneori neasteptate, insa in nici un caz structurate. Ca sa nu mai spun ca fara laptop sunt un om nenorocit. Toate cifrele (ratinguri, procente, profile) pe care ar trebui sa le tin in minte le am in computador...
:)
Dar un lucru imi amintesc clar. Imi este infipt in minte ca un cui de puscarias: demonstratia faptului ca un numar irational ridicat la o putere irationala poate da un numar rational. Este de o eleganta dureroasa. Simpla, clara, fara nici un fel de fortare ori de formula. Logica precum sus, in Olymp, cand se imbata aia cu hidromel si vad tot universul in buza unui pahar.
Ascultati aici:
Sa luam numarul a = radical(2) la puterea radical(2). Avem doua variante:
a micutz) acest numar radical(2) la puterea radical(2) este rational. Atunci quod erat demonstrandum. Hai la bere. Se poate: un numar irational (radical(2), ca stim deja asta, din alte demonstratii, ca este irational), ridicat la el insusi, adica tot la un numar irational, da ceva rational. La bere, am zis. Gata cu matematica...
b micutz) sa zicem ca a nu este rational. Atunci sa'l ridicam la puterea radical(2). Deci un numar irational (a) ridicat la alta putere irationala (radical(2).
Ce rezulta?
Pai a la puterea radical(2) = [radical(2) la puterea radical(2)] totul la puterea radical(2). Dupa cum stim: (x la puterea y) totul la puterea z = x la puterea y ori z. Deci obtinem: radical(2) la puterea (radical(2) ori radical(2). Adica radical din doi la puterea doi. Adica doi. Adica un numar rational.
Din nou quod erat demonstrandum. A treia cale nu se exista. Numarul a este ori rational, ori irational. Oricum ai da-o, gasesti un numar irational la o putere irationala care sa iti dea ceva rational.
Dupa cum va spuneam: demonstratia este fara de cusur. Si de o eleganta dureroasa. Principala frumusete este ca, plecand de la o slabiciune (nu stim daca numarul a este irational sau nu) si folosindu-ne doar de ascutimea mintii, nu de forta bruta a unor calcule ori demonstratii complicate si pline de semne filiforme, o scoti la capat intr-o jumatate de pagina. Ce am scris eu aici e lung, pentru ca nu am la dispozitie semnele matematice (radical, rezulta, alea alea).
Vedeti? E frumoasa matematica. Chiar si cand nu mai stii mare lucru din ea...
:)
Courtesy of Dan Selaru, care mi'a facut pofta de creion si de hartie.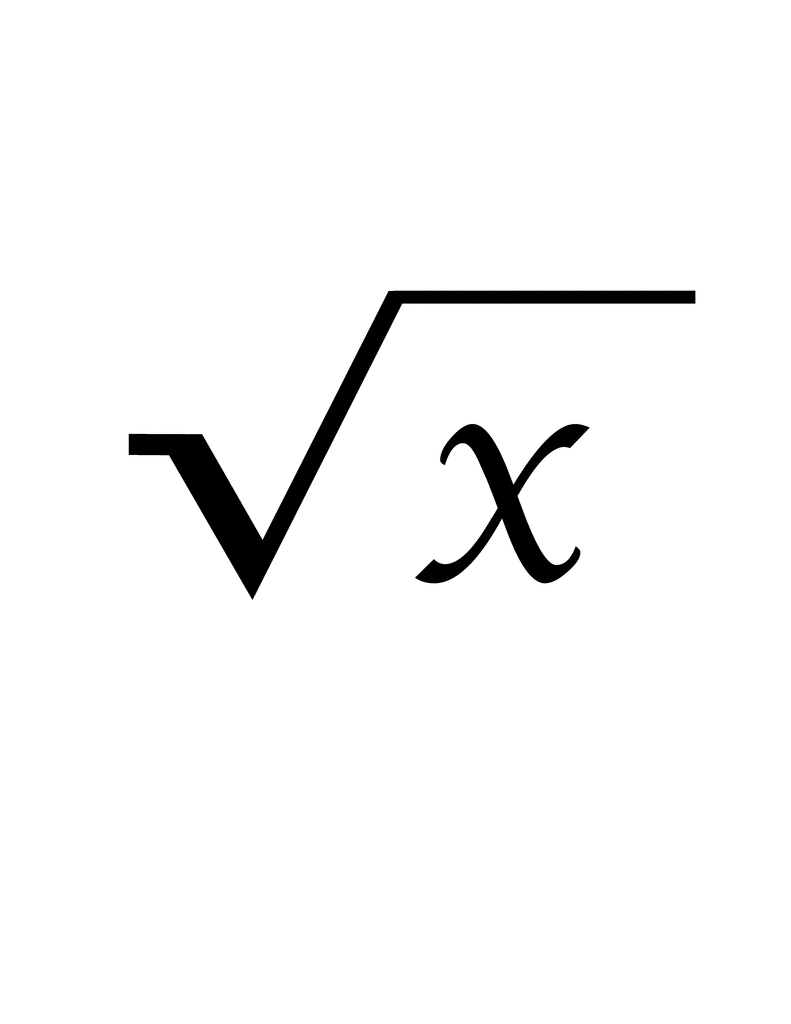
Știrile zilei – 5 martie 2026
Acum 2 ore




2 comentarii:
si orice nr ridicat la puterea "0" este "1",frumoasa si profunda matematica,nu degeaba e mana-n mana cu filozofia si logica stimabile domn :)
Acum am vazut. Misto. e unul din lucrurile cele mai frumoase, inainte de a trage cu tunul sa gandesti.
Trimiteți un comentariu